Examples

A series of typical usage scenarios are given, including the result and the source code.

Note

  • Three different model systems are used in the examples below. More information on these model systems can be found under Model systems.

  • The examples below can be reproduced from the electron density files as stored in dataset.tar.bz2 which can be found under src/test/testinput.

  • It is assumed that the executable edp is available from the $PATH.

Electron density projection

Consider the benzene molecule, centered in a rectangular unit cell with dimensions 14.313320 Å x 14.980580 Å x 10.000000 Å. To generate a projection of the electron density onto a plane spanned by the normal vectors \(\vec{v} = (1,0,0)\) and \(\vec{w} = (0,1,0)\) going through the center of the unit cell, the following command in run:

edp -i PARCHG_BENZENE_07 -o benzene_xy.png \
-p 7.15666,7.49029,5.0 -v 1,0,0 -w 0,1,0 -s 25
Projection of the electron density of benzene through the xy plane.

If no bounds are set, the electron density is by default projected according to \(\rho \in (10^{-7},10^{2})\).

Setting bounds and adding legend

To set the bounds of the electron density to \(\rho \in (10^{-5},10^{0})\) and add a legend to the plot, the following command is used:

edp -i PARCHG_BENZENE_07 -o benzene_xy.png \
-p 7.15666,7.49029,5.0 -v 1,0,0 -w 0,1,0 -s 25 -b -5,0 -l
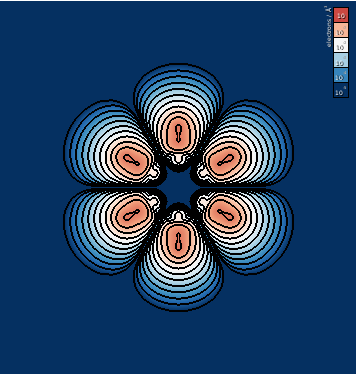
Projection of the electron density of benzene through the xy plane including legend and setting new bounds.

Instead of specifying the center of unit the unit cell by hand, we can perform the same operation by using atom indices. Since all the atoms lie on the \(xy\)- plane through the center of the unit cell, we can pick any atom. Here, we have used the first atom:

edp -i PARCHG_BENZENE_07 -o benzene_xy.png -p 1 -v 1,0,0 -w 0,1,0 -s 25 -b -5,0 -l

Specifying a different plane

To produce the projection onto the \(xz\)-plane through the first carbon atom, the following command is used:

edp -i PARCHG_BENZENE_07 -v 1,0,0 -w 0,0,1 -s 25 -p 1 -o benzene_xz.png -b -5,0 -l
Projection of the electron density of benzene through the xz plane.

Increasing projection plane size

To increase the scale of the image, we can use 30 pixels/Å instead of 25 pixels/Å as used in the previous examples:

edp -i PARCHG_BENZENE_07 -v 1,0,0 -w 0,0,1 -s 30 -p 1 -o benzene_xz.png -b -5,0 -l
Projection of the electron density of benzene through the xz plane.

Color schemes

EDP supports 16 color schemes as schematically shown in the image below. To select a color scheme, append the following to the command line instructions: -c <color-scheme-id> where <color-scheme-id> should be a number between 0-15, inclusive.

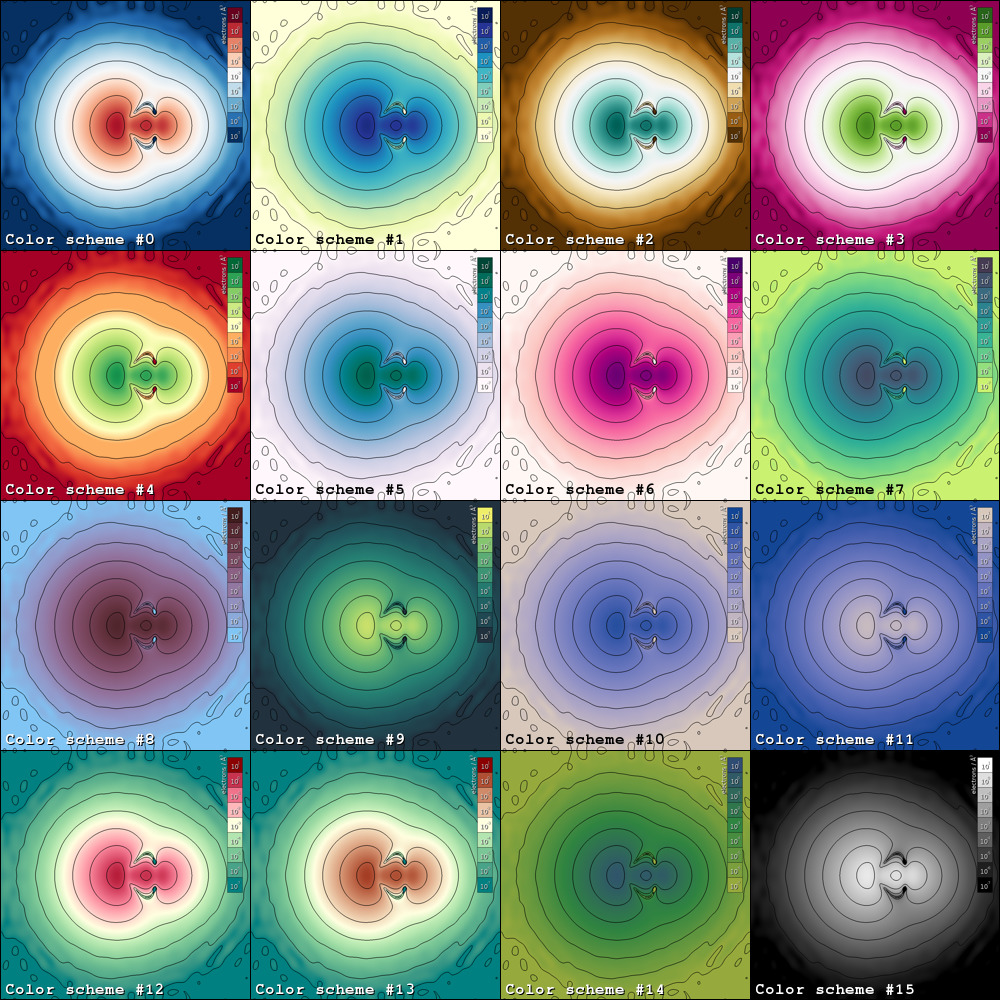
Set of 16 different color schemes.

Note

The color schemes are extracted from the following resources.

Special features

Note

In the subsections below, a list of special features of EDP is given. To visualize the results, we have made use of NumPy and Matplotlib. These programs are typically readily available on Linux operating systems. The scripts used below can be found in the examples folder on Github.

Z-averaging

Consider the \((111)\;2x2\) termination of FCC Al using 7 layers. Besides projecting the electron density onto the plane, we can supply an additional instruction to calculate the total electron density per plane lying in the \(z\)-direction:

edp -i CHGCAR_Al_FCC111 -o al_fcc111_xz.png \
-p 28 -v 1,0,0 -w 0,0,1 -s 25 -b -5,0 -l -z

The result is stored in z_extraction.txt which can be readily visualized using a simple Python script.

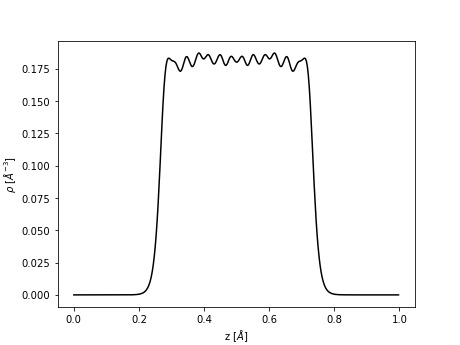
Electron density at height z.

Line extraction

Consider the methane molecule at the center of a cubic unit cell of length 10 Å. We wish to calculate the average electron density alongside a line running through the central carbon atom to one of the H atoms:

edp -i CHGCAR_CH4 -o ch4.png \
-p 1 -v 1,0,0 -w 0,1,0 -s 25 -e 1-2

The result is stored in line_extraction.txt.

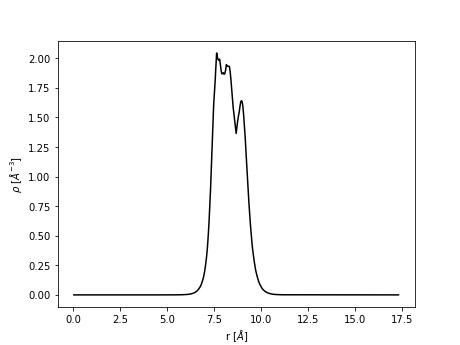
Electron density alongside C-H coordinate in methane.

Note that the electron density is plotted between 0 and ~17.5 Å. This corresponds to the tridiagonal of the cubic unit cell which has size \(\sqrt{3} * 10 \approx 17.32\) Å.

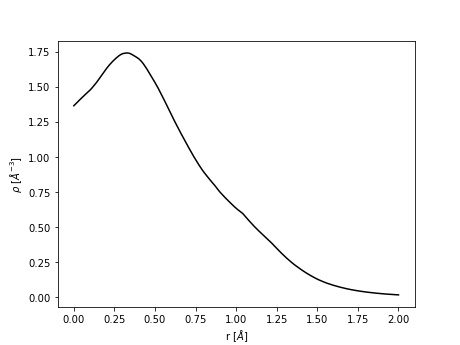
Spherical averaging

Consider the methane molecule at the center of a cubic unit cell of length 10 Å. We wish to calculate the average electron density surrounding the central carbon atom. This can be done using:

edp -i CHGCAR_CH4 -o ch4.png \
-p 1 -v 1,0,0 -w 0,1,0 -s 25 -r 1,2

The result is stored in spherical_average.txt.

Average electron density at radial position r surrounding C in methane.

Model systems

In the examples as shown on this page, three model systems have been used. The files to reproduce these calculations can be found here.

Benzene

Benzene molecule inside its unit cell. 
 1 C  H                                   
 2   1.0000000000000000     
 3    14.3133200000000009    0.0000000000000000    0.0000000000000000
 4     0.0000000000000000   14.9805799999999998    0.0000000000000000
 5     0.0000000000000000    0.0000000000000000   10.0000000000000000
 6   C    H 
 7     6     6
 8Direct
 9  0.5000000000000000  0.5933244878604808  0.5000000000000000
10  0.4154116501391032  0.5466643642949370  0.5000000000000000
11  0.4154116501391032  0.4533356357050631  0.5000000000000000
12  0.5000000000000000  0.4066755121395193  0.5000000000000000
13  0.5845883498608969  0.4533356357050631  0.5000000000000000
14  0.5845883498608969  0.5466643642949370  0.5000000000000000
15  0.5000000000000000  0.6661748879618772  0.5000000000000000
16  0.3493793251819203  0.5830873759075694  0.5000000000000000
17  0.3493793251819203  0.4169126240924306  0.5000000000000000
18  0.5000000000000000  0.3338251120381229  0.5000000000000000
19  0.6506206748180797  0.4169126240924306  0.5000000000000000
20  0.6506206748180797  0.5830873759075694  0.5000000000000000

Methane

Methane molecule inside its unit cell. 
 1CH4                                     
 2   1.0000000000000000     
 3    10.0000000000000000    0.0000000000000000    0.0000000000000000
 4     0.0000000000000000   10.0000000000000000    0.0000000000000000
 5     0.0000000000000000    0.0000000000000000   10.0000000000000000
 6   C    H 
 7     1     4
 8Direct
 9  0.5000000000000000  0.5000000000000000  0.5000000000000000
10  0.4366541535484265  0.4366541535484265  0.4366541535484265
11  0.5633458464515737  0.5633458464515736  0.4366541535484265
12  0.4366541535484265  0.5633458464515737  0.5633458464515736
13  0.5633458464515736  0.4366541535484265  0.5633458464515737

Aluminium FCC(111)

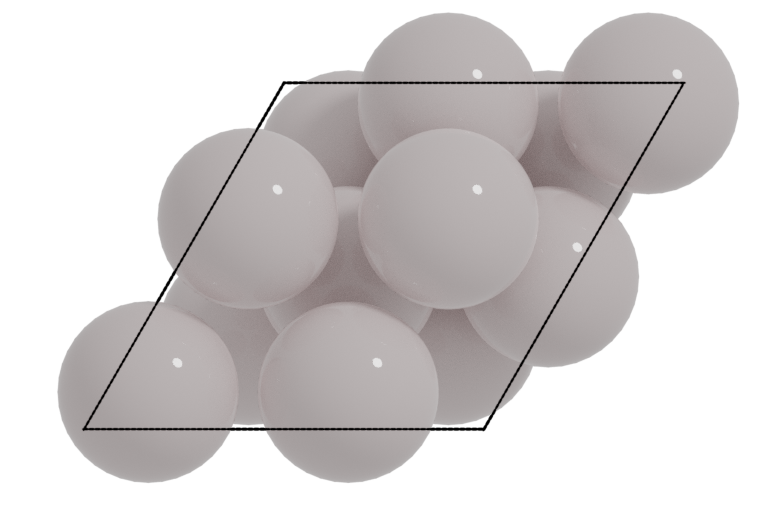
(111) termination of Al/FCC bulk. 
 1Al                                      
 2   1.0000000000000000     
 3     5.7275649276110352    0.0000000000000000    0.0000000000000000
 4     2.8637824638055176    4.9602167291359347    0.0000000000000000
 5     0.0000000000000000    0.0000000000000000   34.0296115413079079
 6   Al
 7    28
 8Direct
 9  0.0000000000000000 -0.0000000000000000  0.2948892147472962
10  0.5000000000000000 -0.0000000000000000  0.2948892147472962
11  0.0000000000000000  0.5000000000000000  0.2948892147472962
12  0.5000000000000000  0.5000000000000000  0.2948892147472962
13  0.1666666666666643  0.1666666666666643  0.3640369018627199
14  0.6666666666666643  0.1666666666666643  0.3640369018627199
15  0.1666666666666643  0.6666666666666643  0.3640369018627199
16  0.6666666666666643  0.6666666666666643  0.3640369018627199
17  0.8333333333333357  0.3333333333333357  0.4317507348766002
18  0.3333333333333357  0.3333333333333357  0.4317507348766002
19  0.8333333333333357  0.8333333333333357  0.4317507348766002
20  0.3333333333333357  0.8333333333333357  0.4317507348766002
21  0.0000000000000000 -0.0000000000000000  0.5000000000000000
22  0.5000000000000000 -0.0000000000000000  0.5000000000000000
23  0.0000000000000000  0.5000000000000000  0.5000000000000000
24  0.5000000000000000  0.5000000000000000  0.5000000000000000
25  0.1666666666666643  0.1666666666666643  0.5682492651233999
26  0.6666666666666643  0.1666666666666643  0.5682492651233999
27  0.1666666666666643  0.6666666666666643  0.5682492651233999
28  0.6666666666666643  0.6666666666666643  0.5682492651233999
29  0.8333333333333357  0.3333333333333357  0.6359630981372800
30  0.3333333333333357  0.3333333333333357  0.6359630981372800
31  0.8333333333333357  0.8333333333333357  0.6359630981372800
32  0.3333333333333357  0.8333333333333357  0.6359630981372800
33  0.0000000000000000 -0.0000000000000000  0.7051107852527040
34  0.5000000000000000 -0.0000000000000000  0.7051107852527040
35  0.0000000000000000  0.5000000000000000  0.7051107852527040
36  0.5000000000000000  0.5000000000000000  0.7051107852527040